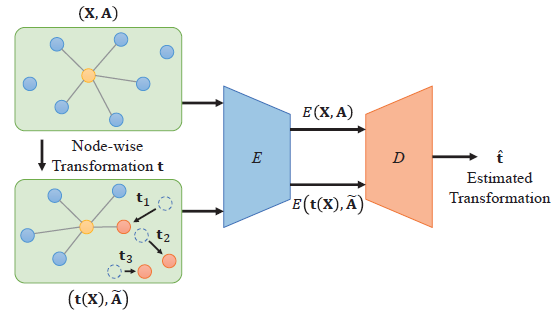
Recent advances in Graph Convolutional Neural Networks (GCNNs) have shown their efficiency for nonEuclidean data on graphs, which often require a large amount of labeled data with high cost. It it thus critical to learn graph feature representations in an unsupervised manner in practice. To this end, we propose a novel unsupervised learning of Graph Transformation Equivariant Representations (GraphTER), aiming to capture intrinsic patterns of graph structure under both global and local transformations. Specifically, we allow to sample different groups of nodes from a graph and then transform them node-wise isotropically or anisotropically. Then, we self-train a representation encoder to capture the graph structures by reconstructing these node-wise transformations from the feature representations of the original and transformed graphs.
这段话意思就是:现在GCN在非欧式数据(比如点云)上有很好的效果,但图结构标注数据量过大,所以提出用无监督的方式(自编码器)学一个变换,从而能在被全局变换或者局部变换后的的数据上也能提取到相对应的图结构
where f() is a linear or non-linear function applied to each pair of nodes to get the pair-wise similarity. For example,a widely adopted function is to nonlinearly construct a k-nearest-neighbor (kNN) graph from node features
和pointnet系列的文章一样,图的边权是通过KNN(k个最近的点与中心点的差)+MLP(多层感知机)提取到的
Formally, suppose we sample a graph transformation t from a transformation distribution Tg, i.e., t $\sim$ Tg. Applying the transformation to graph signals X that are sampled from data distribution Xg, i.e., X $\sim$ Xg, leads to the filtered graph signal
对变换方式的分布进行采样 并对图数据信号进行变换,则得到变换后的图信号
以及变换后的图结构
然后对变换前的点云$X$和变换后的点云$\tilde{X}$在共享的encoder中做GCN,
encoder得到的特征图中第i个点的特征$a_{i,j}$是 通过 第i个节点特征+ 邻域节点j特征相对原特征的偏移量 并作非线性映射后的最大的边特征
这个公式打不出来 qaq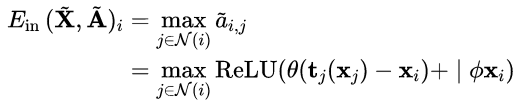
在encoder后的bottleneck处把$X_{output}和\widetilde{X}_{output}$做拼接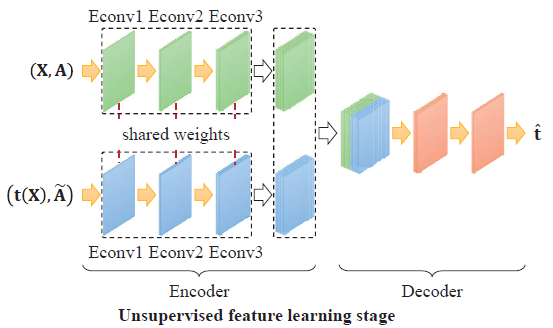
Node-wise features of the original and transformed graphs are then concatenated at each node, which are then fed into the transformation decoder. The decoder consists of several EdgeConv blocks to aggregate the representations of both the original and transformed graphs to predict the nodewise transformations t. Based on the loss in (5), t is decoded by minimizing the mean squared error (MSE) between the ground truth and estimated transformation parameters at each sampled node. Fig. 4 illustrates the architecture of learning the proposed GraphTER in such an auto-encoder structure.
decoder也是GCN提特征最后得到变换量的预测$\hat{t}$,
并且我们将预测得到的变换图$\widetilde{t} (N×3)$与t$(N×3)$的均方根误差最小化,通过变化量的loss更新encoder和decoder,
In the unsupervised feature learning stage, the representation encoder and transformation decoder are jointly trained by minimizing (5).In the supervised evaluation stage, the first several blocks of the
encoder are fixed with frozen weights and a linear classifier is trained with labeled samples.
第一个阶段我们并没有训练encoder去把每个点的类别分开,而只是通过学习变换量使得我们的encoder在面对带变换的数据时仍然能提取到依然有效的图结构及图特征(对于新的数据更鲁棒)。
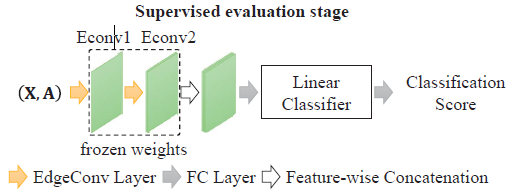
在第二个阶段,将前几层encoder冻结,接近分类器的层的权重能通过梯度更新做下游任务(分割,分类)。



