Bayesian network贝叶斯神经网络及其改进

秋招补一下Intel实习期间看的东西

经典的神经网络一般是最大化数据集$\mathcal{D}=(x_i,y_i)$下的最大似然$P(\mathcal{D} \mid \mathbf{w})$ ，即在网络权重为$w$时让输入$x_i$时输出$y_i$的概率最大

$$\begin{aligned} \mathbf{w}^{\text {MLE }} &=\arg \max _{\mathbf{w}} \log P(\mathcal{D} \mid \mathbf{w}) \\ &=\arg \max _{\mathbf{w}} \sum_{i} \log P\left(\mathbf{y}_{i} \mid \mathbf{x}_{i}, \mathbf{w}\right) \end{aligned}$$

如果给网络权重$w$一个先验概率分布，则相当于求最大后验，通过转化相当于最大似然+先验正规化，对于高斯先验($L_2$范数正则)，对于拉普拉斯先验($L_1$范数正则)

$$\begin{aligned} \mathbf{w}^{\text {MAP }} &=\arg \max _{\mathbf{w}} \log P(\mathbf{w} \mid \mathcal{D}) \\ &=\arg \max _{\mathbf{w}} \log P(\mathcal{D} \mid \mathbf{w})+\log P(\mathbf{w}) \end{aligned}$$

但通过最大似然或最大后验学出来的都是权重$w$的定值，那么我们如果想知道$w$的分布应该怎么办呢？

ICML 2015 Weight Uncertainty in Neural Networks这篇论文做了相关的工作

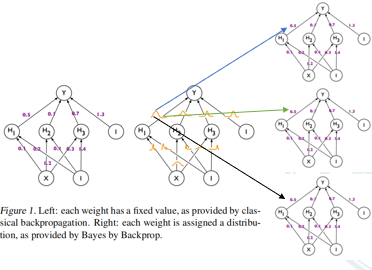
左边的一般的神经网络的权重每次更新后是一个定值，右边的神经网络的权重是一个分布，是一个随机变量

• 第一个问题：怎么去表示这样的权重？这篇文章的做法是将训练一个网络转化为训练一个网络集合

  具体的：文章假设权重符合高斯分布，那么对于每个权重都有一个均值μ和方差σ，然后对这样的分布进行采样，每种采样就对应网络集合中的一个网络，更具体的说就是，前向传播的时候我一个网络架构对每个权重同时进行采样，每种采样都前传一次，然后损失加起来。这个$\sigma$相当于给了模型预测的置信度

• 第二个问题：这样的直接采样$N(\mu,\sigma)$的话μ和σ都是不可微的

  所以引入重参数化trick，具体的就是将采样交给一个标准正态分布$\epsilon$ ~ $N(0,1)$去做，σ就转化为一个正的scale乘上$\epsilon$,μ此时也可看作是一个常量，那么此时的μ和ρ就是可微的了，问题转化为学一个μ和ρ

$$w=\mu+\sigma \times \epsilon=\mu+\log \left(1+e^{\rho}\right) \times \epsilon$$

对于测试集中的数据$\hat x$拔和$\hat y$，预测分布$P(\hat y|\hat x)$就等价于我们刚刚提到的网络集合里 每种权重的后验概率$P(w|D)$ 及 该权重对测试集数据的预测概率$P(\hat y|\hat x)$的 加权，即表示成每种权重的后验概率$P(w|D)$下$P(\hat y|\hat x)$的期望

$$P(\hat{\mathbf{y}} \mid \hat{\mathbf{x}})=\mathbb{E}_{P(\mathbf{w} \mid \mathcal{D})}[P(\hat{\mathbf{y}} \mid \hat{\mathbf{x}}, \mathbf{w})]$$

回顾贝叶斯公式

$$P(w \mid D)=P(D \mid w) * P(w) / P(D) \\ P(D)=\sum_{w} P(D \mid w) * P(w) \\ P(w \mid D) = \frac{P(D \mid w) * P(w)}{\sum_{w} P(D \mid w) * P(w)}$$

问题是这个后验很难求，我们不可能对所有可能的$w$的先验$P(w)$和它对应的似然$P(D \mid w)$进行加权，那么这篇文章就提出通过变分近似的方法学一个参数$θ$,并最小化在$θ$下$w$的分布$q(\mathbf{w} \mid \theta)$和$w$在训练集上的后验分布$P(\mathbf{w} \mid \mathcal{D})$的$KL$距离,那么在$θ$参数化下的网络去采样的时候就近似了我们的后验分布$P(\mathbf{w} \mid \mathcal{D})$

$$\begin{aligned} \theta^{\star} &=\arg \min _{\theta} \mathrm{KL}[q(\mathbf{w} \mid \theta) \| P(\mathbf{w} \mid \mathcal{D})] \\ &=\arg \min _{\theta} \int q(\mathbf{w} \mid \theta) \log \frac{q(\mathbf{w} \mid \theta)}{P(\mathbf{w}) P(\mathcal{D} \mid \mathbf{w})} \mathrm{d} \mathbf{w} \\ &=\arg \min _{\theta} \mathrm{KL}[q(\mathbf{w} \mid \theta) \| P(\mathbf{w})]-\mathbb{E}_{q(\mathbf{w} \mid \theta)}[\log P(\mathcal{D} \mid \mathbf{w})] \end{aligned}$$

转化后的最后的表达式中第一项最小化参数$θ$下$w$的分布$q(\mathbf{w} \mid \theta)$和先验$P(w)$的$KL$距离，第二项尽量大就保证采样出来的$w$可以在训练集上最大似然

当我们的$\theta$定义为μ和ρ的时候，我们就能实现通过优化上述表达式得到权重$w$的后验分布

talk is cheap,show me your code

code
torch版 by Intel Research Lab的大佬

首先实现了一个基础变分层类，里面主要只有一个函数kl_div用来计算两个正态分布的KL散度，这个式子的话是从两个正态分布的对数期望通过简化后的表达式

$$\begin{aligned} \mathrm{KL}(q \| p) &=\mathrm{E}_{q}\left[\log \frac{\frac{1}{\sqrt{2 \pi \sigma_{1}}} \exp \left(-\frac{\left(X-\mu_{1}\right)^{2}}{2 \sigma_{1}^{2}}\right)}{\frac{1}{\sqrt{2 \pi \sigma_{2}}} \exp \left(-\frac{\left(X-\mu_{2}\right)^{2}}{2 \sigma_{2}^{2}}\right)}\right] \\ &=\mathrm{E}_{q}\left[\log \sigma_{2}-\log \sigma_{1}-\frac{\left(X-\mu_{1}\right)^{2}}{2 \sigma_{1}^{2}}+\frac{\left(X-\mu_{2}\right)^{2}}{2 \sigma_{2}^{2}}\right] \\ &=\log \sigma_{2}-\log \sigma_{1}+\mathrm{E}_{q}\left[\frac{\left(X-\mu_{2}\right)^{2}}{2 \sigma_{2}^{2}}\right]-\mathrm{E}_{q}\left[\frac{\left(X-\mu_{1}\right)^{2}}{2 \sigma_{1}^{2}}\right] \end{aligned}$$ $$\begin{aligned} &\mathrm{E}_{q}\left[\frac{\left(X-\mu_{1}\right)^{2}}{2 \sigma_{1}^{2}}\right]=\frac{\sigma_{1}^{2}}{2 \sigma_{1}^{2}}=\frac{1}{2} \\ &\mathrm{E}_{q}\left[\frac{\left(X-\mu_{2}\right)^{2}}{2 \sigma_{2}^{2}}\right]=\mathrm{E}_{q}\left[\frac{\left(X-\mu_{1}+\mu_{1}-\mu_{2}\right)^{2}}{2 \sigma_{2}^{2}}\right]=\frac{\sigma_{1}^{2}+\left(\mu_{1}-\mu_{2}\right)^{2}}{2 \sigma_{2}^{2}} \end{aligned}$$ $$\mathrm{KL}(q \| p)=\log \sigma_{2}-\log \sigma_{1}+\frac{\sigma_{1}^{2}+\left(\mu_{1}-\mu_{2}\right)^{2}}{2 \sigma_{2}^{2}}-\frac{1}{2}$$

重参数化卷积的具体实现，

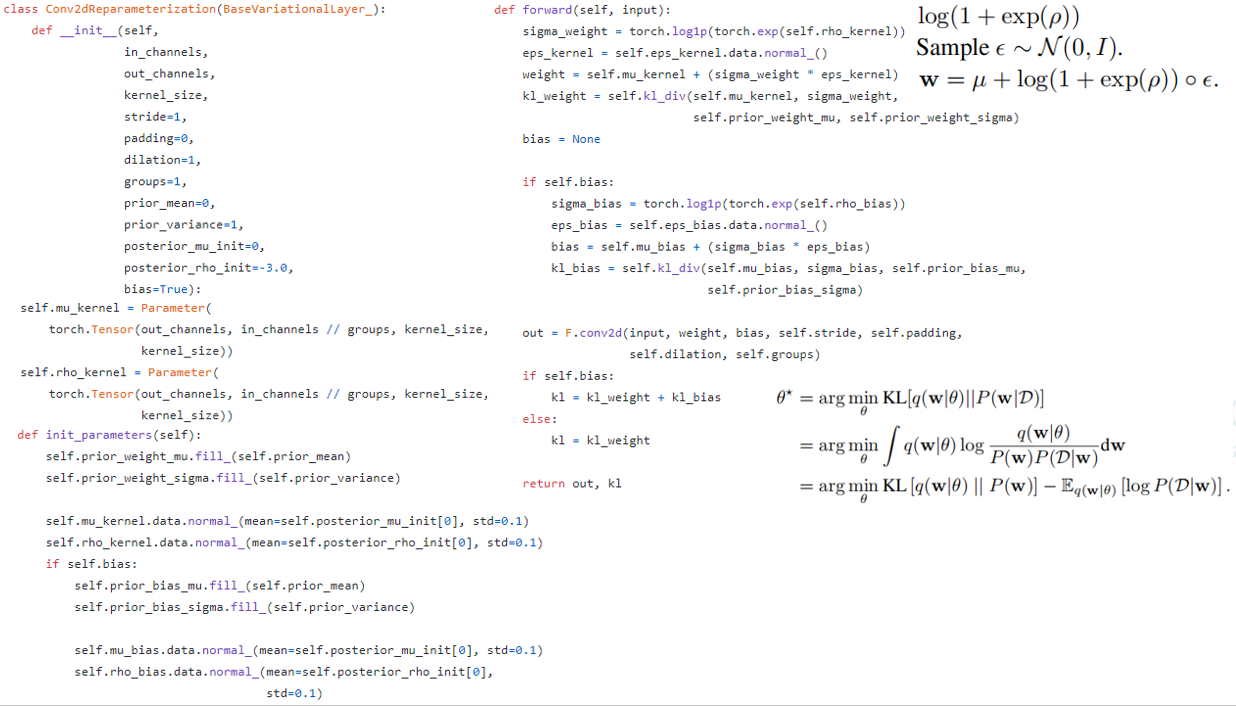
他首先继承了刚刚的基础变分层类，从而可以计算训练集下后验$P(w\mid D)$和参数θ下$q(w|\theta)$的kl散度

首先他根据输入输出的特征层数，卷积核的尺寸定义了我们刚刚那个式子里每个权重的μ和ρ，通过torch.nn的Parameter这个类转化为可学的参数

初始化参数的时候通过输入的先验μ和先验σ初始化先验分布

通过输入的初始后验μ和σ和0.1的标准差初始化θ参数化下的后验μ和后验σ

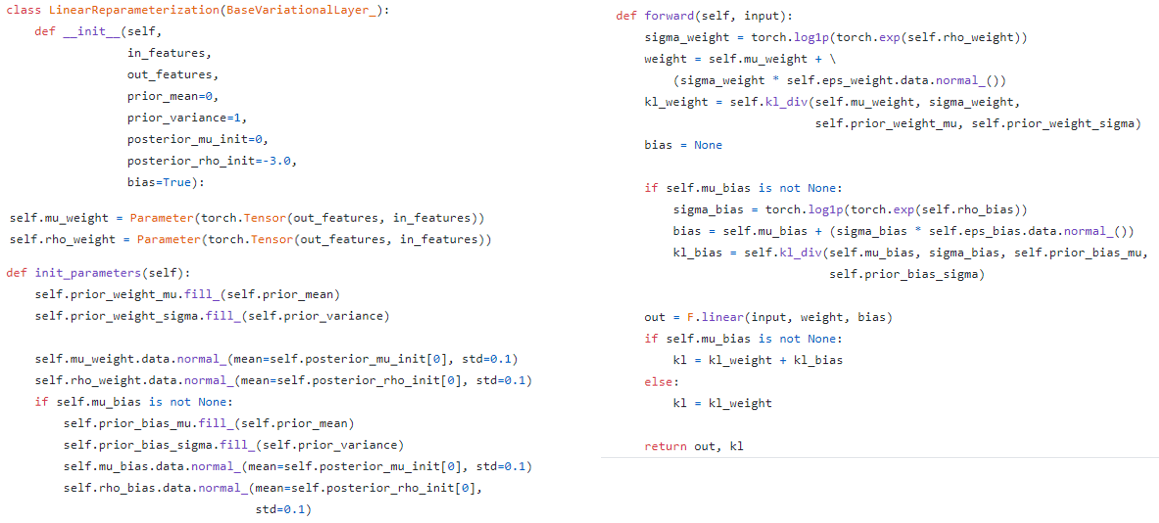
线性层同理

则Resnet的一个BasicBlock的BNN形式如下，在前传的时候将各个Linear和Conv的kl损失累加起来

class BasicBlock(nn.Module):
    expansion = 1

    def __init__(self, in_planes, planes, stride=1, option='A'):
        super(BasicBlock, self).__init__()
        self.conv1 = Conv2dReparameterization(
            in_channels=in_planes,
            out_channels=planes,
            kernel_size=3,
            stride=stride,
            padding=1,
            prior_mean=prior_mu,
            prior_variance=prior_sigma,
            posterior_mu_init=posterior_mu_init,
            posterior_rho_init=posterior_rho_init,
            bias=False)
        self.bn1 = nn.BatchNorm2d(planes)
        self.conv2 = Conv2dReparameterization(
            in_channels=planes,
            out_channels=planes,
            kernel_size=3,
            stride=1,
            padding=1,
            prior_mean=prior_mu,
            prior_variance=prior_sigma,
            posterior_mu_init=posterior_mu_init,
            posterior_rho_init=posterior_rho_init,
            bias=False)
        self.bn2 = nn.BatchNorm2d(planes)

        self.shortcut = nn.Sequential()
        if stride != 1 or in_planes != planes:
            if option == 'A':
                """
                For CIFAR10 ResNet paper uses option A.
                """
                self.shortcut = LambdaLayer(lambda x: F.pad(
                    x[:, :, ::2, ::2],
                    (0, 0, 0, 0, planes // 4, planes // 4), "constant", 0))
            elif option == 'B':
                self.shortcut = nn.Sequential(
                    Conv2dReparameterization(
                        in_channels=in_planes,
                        out_channels=self.expansion * planes,
                        kernel_size=1,
                        stride=stride,
                        prior_mean=prior_mu,
                        prior_variance=prior_sigma,
                        posterior_mu_init=posterior_mu_init,
                        posterior_rho_init=posterior_rho_init,
                        bias=False), nn.BatchNorm2d(self.expansion * planes))
    def forward(self, x):
        kl_sum = 0
        out, kl = self.conv1(x)
        kl_sum += kl
        out = self.bn1(out)
        out = F.relu(out)
        out, kl = self.conv2(out)
        kl_sum += kl
        out = self.bn2(out)
        out += self.shortcut(x)
        out = F.relu(out)
        return out, kl_sum

训练的时候通过mento carlo采样 kl散度项损失

def train(args, model, device, train_loader, optimizer, epoch, tb_writer=None):
    model.train()
    for batch_idx, (data, target) in enumerate(train_loader):
        data, target = data.to(device), target.to(device)
        optimizer.zero_grad()
        output_ = []
        kl_ = []

        for mc_run in range(args.num_mc):
            output, kl = model(data)
            output_.append(output)
            kl_.append(kl)
        
        output = torch.mean(torch.stack(output_), dim=0)
        kl = torch.mean(torch.stack(kl_), dim=0)
        nll_loss = F.nll_loss(output, target)
        #ELBO loss
        loss = nll_loss + (kl / args.batch_size)

        loss.backward()
        optimizer.step()

        if batch_idx % args.log_interval == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                100. * batch_idx / len(train_loader), loss.item()))

        if tb_writer is not None:
            tb_writer.add_scalar('train/loss', loss.item(), epoch)
            tb_writer.flush()